Notes on 'Non-linear PCA' I: On Variational Autoencoders

Introduction

This is part one of my “Notes on ‘Non-linear PCA” blog article series, where I discuss various deep generative modeling techniques. The series is based on a project that I worked on for Stanford’s CS168, along with Ada Zhou, Chris Rilling, and Devorah Rena Simon. This project was originally titled “Notes on ‘Non-linear PCA’ for Deep Generative Modeling: VAEs, GANs, and DDPMs for Modelling Complex Data Distributions.”

Deep generative modelling is a problem that has gained much prominence over the past few years, with the developments of image synthesis services such as OpenAI’s DALLE2 and Stability AI’s Stable Diffusion. The goal of deep generative modelling is to use existing samples of some dataset to approximate the complex data distribution that generated said dataset in order to generate new, previously-unseen samples from that distribution. Here, we present three popular methods to model complex data distributions: VAEs, GANs, and DDPMs. The models above assume that there are latent variables that, through some stochastic process, are able generate the data distributions that they attempt to model. In PCA, we attempt to apply dimensionality reduction to a dataset in order to uncover latent structure within it. However, this method has limitations due to the fact that it is only able to uncover linear relationships in this way. Moreover, PCA isn’t really a suitable method to construct new examples from the same data distribution generating whatever dataset it is applied on. All of the models stated overcome these limitations due to their ability to harness deep neural networks, which are able to capture these non-linear relationships, and thus war- rant further study.

Before jumping into VAEs, it’s important to talk about autoencoders first.

Vanilla Autoencoders

Autoencoders can be thought of as nonlinear PCA. They basically are two neural networks that encode datapoints into some lower-dimensional representation, and then decode them. They have two autoencoders, an encoder and a decoder. Like PCA, autoencoders have been used for dimensionality reduction.

More formally, given a sample $x$ from a distribution, we have two neural networks $f$ and $g$. $f$ serves as an encoder function which produces a code $h = f(x)$, and $g$ serves as a decoder function which produces a reconstruction $r = g(h)$. The goal of an autoencoder is to set $g(f(x))$ as close to $x$ given some loss function $L$, such as mean squared error loss. The goal is to let $h$ have smaller dimensionality than the input dimension (doing so makes the autoencoder undercomplete). By making the autoencoder undercomplete, we force the autoencoder to capture the most important features driving the training data ¹.

Autoencoders with linear decoders and mean squared error as $L$ learn to span the same subspace as PCA. Learning to do the copying task amounts to learning the principal subspace of the training data as the side effect. If the autoencoder has nonlinear encoder and decoder functions, they can learn more powerful representations compared to PCA. Having too much capacity means that they can map outputs to inputs without extracting useful information about the distribution of the training data. Given powerful enough encoders and decoders with one-dimensional code, it’s possible for the encoder to map each training example $x^{(i)}$ to some code $i$, and for the decoder to reconstruct code $i$ back into the specific training example that generated that code ².

Improving Autoencoders via Probability

With traditional autoencoders, a sample is generated by inputting some code $z$ into the decoder $g$. With variational autoencoders, however, instead of encoding a specific variable, you try to encode a $\textit{distribution}$; we instead sample a code from the code distribution $p_{model}(z)$; the sample is fed though the decoder network $g(z)$; here, the twist is that instead of getting back a sample from the data distribution we’re trying to model, we instead get back another data distribution $p_{model}(x; g(z)) = p_{model}(x | z)$ from our encoder, and then sample $x$ from this. During training, the encoder $q(z | x)$ is used to obtain $z$ and $p_{model}(x | z)$ is viewed as a decoder network. Variational autoencoders can be thought of as a probabilistic variation of autoencoders where we are able to more easily sample from the model to generate data.

In the problem setup, we assume that we have a dataset $\mathbf{X} = {\mathbf{x}^{(i)}}^N_{i=1}$ of $N$ i.i.d. samples of some continuous random variable $\mathbf{x}$ generated from some random process involving an unobserved variable $\bf{z}$. We also assume that $\mathbf{z}$ has lower dimensionality than $\mathbf{x}$. This process is carried out in the following two steps:

1. Generate $\mathbf{z}^{(i)}$ from some prior distribution $p({\mathbf{z}}).$
2. Generate $\mathbf{x}^{(i)}$ from some conditional distribution $p(\mathbf{x} | \mathbf{z})$ ³.

This means that there exists a joint probability distribution over $\mathbf{x}$ and $\mathbf{z}$ given by: $$p(\mathbf{x}, \mathbf{z}) = p(\mathbf{x} | \mathbf{z}) p(\mathbf{z})$$ This joint probability distribution is ultimately what we wish to model. An example of such a joint probability distribution is one where $\mathbf{x}$ represents an image, and $\mathbf{z}$ encodes latent factors used to generate $\mathbf{x}$: things like attributes, orientation, etc.

Now, consider a family of distributions $\mathcal{P}_\mathbf{z}$ where $p(\mathbf{z}) \in \mathcal{P}_\mathbf{z}$ describes a probability distribution over $\mathbf{z}.$ Next, consider a family of conditional distributions $\mathcal{P}_{\mathbf{x}, \mathbf{z}}$ parameterized by $\theta$, where $p_\theta(\mathbf{x} , \mathbf{z}) \in \mathcal{P}_{\mathbf{x}, \mathbf{z}}$ describes a conditional probability distribution over $\mathbf{x}$ given $\mathbf{z}$. Then our hypothesis class of generative models is the set of all possible combinations

Given this, we are then interested in the two following tasks:

1. Selecting $p_\theta \in \mathcal{P}_{\mathbf{x}, \mathbf{y}}$ that best fits $\mathbf{X}.$
2. Given a sample $\mathbf{x}$ and a model $p_\theta \in \mathcal{P}_{\mathbf{x}, \mathbf{z}}$, find the posterior distribution $p_\theta(z | x)$ over the latent variables $\mathbf{z}$ ⁴.

With respect to task 1, we will need to estimate the true parameters $\theta^*$ of this generative model given our training dataset. To represent this model, we choose a prior $p_\theta({\mathbf{z}})$ to be the centered isotropic unit Gaussian $p_\theta(\mathbf{z}) = \mathcal{N}(\mathbf{z};\mathbf{0}, \mathbf{I})$; this is actually a reasonable choice in the prior distribution if our goal was to model images of faces by capturing latent information such as pose, how much smile, etc. The conditional distribution $p_\theta(\mathbf{x}|\mathbf{z})$ is much more complex, since it constructs $\mathbf{x}$ from the latent variable $\mathbf{z}$ (it would generate an entire image of a face from just latent information); thus, we represent this via a neural network, since neural networks are universal function approximators. We do this by letting

$$ \begin{align*} p_\theta(\mathbf{x} | \mathbf{z}) = \mathcal{N}(\mathbf{x}; \mu_{x|z}(\mathbf{z}), \sigma^2_{x| z} (\mathbf{z}) \mathbf{I}), \end{align*} $$ where $\mu_{x|z}$ and $\sigma^2_{x|z}$ are neural networks. Together, they are referred to as the decoder network. This decoder network models an isotropic multivariate Gaussian ⁵.

The use of the trained decoder network to generate $\mathbf{x}$ once $\theta^*$ is found is shown by the probabilistic graph in \autoref{fig:graphmodel}; if we want to generate $\mathbf{x}^{(i)},$ we sample $\mathbf{z}^{(i)}$ from our prior, feed those through a decoder network to obtain a probability distribution, and then we sample from said probability distribution. This process can be done once we find $p_\theta^*(\mathbf{x}, \mathbf{z})$

In order to do this, we will need to learn the model parameters $\theta^*$ that maximize the likelihood of the training data: $$ \begin{align*} \theta^* &= \argmax_{\theta} \prod_{\mathbf{x} \in \mathbf{X}} p_\theta(\mathbf{x})\\ &= \argmax_{\theta} \prod_{\mathbf{x} \in \mathbf{X}} \int p_\theta(\mathbf{z})p_\theta(\mathbf{x} | \mathbf{z}) d\mathbf{z} \end{align*} $$

The prior distribution $p_\theta(\mathbf{z})$ is a simple Gaussian distribution as specified before, and the likelihood $p(\mathbf{x} | \mathbf{z})$is defined by a decoder neural network, that is differentiable and can thus be optimized. However, there is a problem with the expression above; it is intractable to evaluate because we’d need to integrate over the entire latent space in order to calculate this, which is not computationally feasible since it is infinite.

We can attempt get over this limitation by performing Monte Carlo estimation of this integral for each $\mathbf{x} \in \mathbf{X}$ like so: $$ \begin{align*} \log(p_\theta(\mathbf{x})) \approx \log \frac{1}{k} \sum_{i = 1}^k p_\theta(\mathbf{x} | \mathbf{z}^{(i)}), \text{ where } \mathbf{z}^{(i)} \sim p(\mathbf{z}), \end{align*} $$ but this estimator is too high variance in gradient estimates when training the network. ⁴

The posterior density, which is what we want to obtain in task 2, can be found by using a simple application of Bayes’ rule: $$ \begin{align*} p_\theta(\mathbf{z}|\mathbf{x}) = \frac{p_\theta(\mathbf{x}|\mathbf{z})p_\theta(\mathbf{z})}{p_\theta(\mathbf{x})}. \end{align*} $$ However, it is easily seen that this expression is also intractable because of the denominator term.

The solution to these intractability problems is that in addition to modeling $p_\theta(\mathbf{x}|\mathbf{z})$, we also learn a separate neural network $q_\phi(\mathbf{z}|\mathbf{x} )$ with parameters $\phi$ that approximates the true posterior $p_\theta(\mathbf{z}|\mathbf{x})$. We do this by letting $$ \begin{align*} q_\phi(\mathbf{z} | \mathbf{x}) = \mathcal{N}(\mathbf{z}; \mu_{z|x}(\mathbf{x}), \Sigma_{z|x} (\mathbf{x})), \end{align*} $$ where $\mu_{z|x}$ and $\Sigma_{z|x}$ are neural networks. Together, they are referred to as the encoder network. This encoder network also models a multivariate Gaussian with diagonal covariance structure.

We will see that this approximate posterior allows us to derive a lower bound on the data likelihood that is tractable, which we can optimize for instead.

Variational Inference in VAEs

Variational inference is a technique used to calculate approximations of otherwise intractable posterior distributions given our observed data. Our objective is then to find $\phi^*$ that best approximates the posterior distribution: $$ \begin{align*} \phi^* = \argmin_\phi \text{KL}(q_\phi(\mathbf{z}|\mathbf{x})||p_\theta(\mathbf{z}|\mathbf{x})), \end{align*} $$ where $\text{KL}(\cdot || \cdot)$ denotes the Kullback-Leibler divergence: $$ \begin{align*} \text{KL}\left(q_\phi(\mathbf{z}|\mathbf{x}) , \lvert\lvert , p_\theta(\mathbf{z} | \mathbf{x}) \right) = \int q_\phi(\mathbf{z} | \mathbf{x}) \text{log } \frac{q_\phi(\mathbf{z} | \mathbf{x})}{p_\theta(\mathbf{z} | \mathbf{x})} \mathrm{d}\mathbf{z}\enspace. \end{align*} $$

The KL divergence between our approximate posterior and the true posterior is our objective because it is a measure of how different the two distributions are from each other; low KL-divergence indicates that the two distributions are very similar, while high KL-divergence indicates that they are very different.

Observe that: $$ \begin{align*} &\text{KL}\left(q_\phi(\mathbf{z} | \mathbf{x}) , \lvert\lvert , p_\theta(\mathbf{z} \mid \mathbf{x}) \right) = \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } \frac{q_\phi(\mathbf{z} | \mathbf{x})}{p_\theta(\mathbf{z} | \mathbf{x})}\right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } q_\phi(\mathbf{z} | \mathbf{x}) \right] - \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{z} | \mathbf{x})\right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } q_\phi(\mathbf{z}|\mathbf{x}) \right] - \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } \frac{p_\theta(\mathbf{z}, \mathbf{x})}{p_\theta(\mathbf{x})}\right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } q_\phi(\mathbf{z} | \mathbf{x}) \right] - \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } p_\theta(\mathbf{z}, \mathbf{x})\right]\\ &+ \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } p_\theta(\mathbf{x})\right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } q_\phi(\mathbf{z} | \mathbf{x}) \right] - \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } p_\theta(\mathbf{z}, \mathbf{x})\right] \\ &+ \int q_\phi(\mathbf{z} | \mathbf{x}) \text{log } p_\theta(\mathbf{x}) \mathrm{d}\mathbf{z} \\ &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } q_\phi(\mathbf{z} | \mathbf{x})\right] - \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } p_\theta(\mathbf{z}, \mathbf{x})\right] \\ &+\text{log } p_\theta(\mathbf{x}) \end{align*} $$ The first line re-interprets the integral in the KL divergence as an expectation over $q_\phi(\mathbf{z}|\mathbf{x}).$ The second line applies the log quotient rule and linearity of expectation. The third line uses the definition of conditional probability. The fourth and fifth line apply the log quotient rule and apply linearity of expectation again. The fifth and sixth line use the definition of expectation, and the seventh and last line factor $\log p_\theta(\mathbf{x})$ out of the integral since it is not dependent on $\mathbf{z}$, and the remaining term in the integral evaluates to 1.

Calculating this KL divergence is also problematic because of the $\log p_\theta(\mathbf{x})$ term in the last line, which is intractable.

However, since our goal is to minimize KL divergence, and $\log p_\theta(\mathbf{x})$ is a constant with respect to $\phi$, we can ignore it in our optimization problem. We can then see that $$ \begin{align*} &\text{ELBO}(\phi, \theta) = - \bigg( \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } q_\phi(\mathbf{z} | \mathbf{x})\right]\\ &- \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } p_\theta(\mathbf{z}, \mathbf{x})\right] +\text{log } p_\theta(\mathbf{x}) - \text{log } p_\theta(\mathbf{x}) \bigg)\\ &= \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}\left[\text{log } p_\theta(\mathbf{z}, \mathbf{x})\right] - \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } q_\phi(\mathbf{z} | \mathbf{x})\right]. \end{align*} $$ Note that $$ \begin{align*} &\text{ELBO}(\phi, \theta) = \mathbb{E}_{q_\phi(\mathbf{z} | \mathbf{x})}[\text{log } p_\theta(\mathbf{z}, \mathbf{x})] - \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}[\text{log } q_\phi(\mathbf{z} | \mathbf{x})]\\ &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{x} | \mathbf{z})\right] + \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{z})\right]\\ &- \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } q_\phi(\mathbf{z}|\mathbf{x}) \right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{x} | \mathbf{z})\right] + \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } \frac{p_\theta(\mathbf{z})}{q_\phi(\mathbf{z}|\mathbf{x})}\right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{x} | \mathbf{z})\right] - \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } \frac{q_\phi(\mathbf{z}|\mathbf{x})}{p_\theta(\mathbf{z})}\right] \\ &= \mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{x} | \mathbf{z})\right] - \text{KL}\left(q_\phi(\mathbf{z}|\mathbf{x}) || p_\theta(\mathbf{z})\right) \end{align*} $$ This means that

$$ \begin{align*} \argmin_\phi \text{KL}\left(q_\phi(\mathbf{z} | \mathbf{x}) \lvert\lvert p_\theta(\mathbf{z} | \mathbf{x}) \right) = \argmax_\phi \text{ELBO}(\phi, \theta) \end{align*} $$

This is very interesting, because maximizing this ELBO quantity with respect to $\phi$ lets us find an approximate distribution $q_\phi(\mathbf{z}|\mathbf{x})$ over the latent variables $\mathbf{z}$ that allow us to predict the data well; this is done by maximizing the $\mathbb{E}_{q_\phi(\mathbf{z}|\mathbf{x})}\left[\text{log } p_\theta(\mathbf{x} | \mathbf{z})\right]$ term. At the same time, there is a penalty incurred if $q_\phi(\mathbf{z}|\mathbf{x})$ strays far away from the prior $p_\theta(\mathbf{z})$, which is governed by the $- \text{KL}\left(q_\phi(\mathbf{z}|\mathbf{x}) , \lvert\lvert , p_\theta(\mathbf{z})\right)$ term.

Furthermore, notice that

By definition, $\text{KL}(q_\phi(\mathbf{z}|\mathbf{x})||p_\theta(\mathbf{z}|\mathbf{x}) \geq 0$ , which can then lead us to conclude thatThis is actually a significant result, because if we can’t maximize for $\log p_\theta(x)$ directly, then we can maximize for its lower bound ELBO instead. The terms in equation \eqref{eq:ELBO} can be optimized for, because $p_\theta(\mathbf{x}| \mathbf{z})$ is a differentiable neural network, and because the KL divergence term in equation \eqref{eq:ELBO}is taken between two Gaussians, which has a closed-form solution. This lower bound becomes tighter as our approximate posterior $q_\phi(\mathbf{z} | \mathbf{x})$ gets closer to the true posterior $p_\theta(\mathbf{z} | \mathbf{x})$; the KL divergence term in equation \eqref{eq:used} governs this ⁶.

Thus, we will want to maximize the likelihood lower bound, or the ELBO:

To compute the KL divergence, we’ll use the encoder network to estimate the mean and variance of the gaussian, so we’ll calculate $\mu_{z|x}(\mathbf{z})$ and $\sigma^2_{z|x}(\mathbf{z})$. Because both of the distributions compared in the term are Gaussian, we have a closed-form solution, as discussed earlier. We then compute the conditional log-likelihood with respect to the sampling of the approximate posterior. Here, though, we’d be essentially optimising through a sampling process, which is not part of a computation graph. This is going to pose a problem using traditional optimization methods in deep learning.

Reparametrization Trick

Fortunately, we can use a trick called the reparametrization trick to make the sampling process differentiable: We construct a unit gaussian, sample from it, and construct $\mathbf{z}$ as $$ \begin{align*} \mathbf{z} = \mu_{z|x}(\mathbf{x}^{(i)}) + \epsilon \Sigma_{z|x}(\mathbf{x}^{(i)}), \end{align*} $$ where $\epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{1})$. This way, the graph becomes differentiable.

Once this is calculated, we can then use the decoder network to analytically calculate the log-likelihood of $\mathbf{x}^{(i)}$ by directly using $\mu_{x|z}(\mathbf{z})$ and $\sigma^2_{x|z}(\mathbf{z})$, since $p_\theta(\mathbf{x}|\mathbf{z})$ is a Gaussian distribution. However, in practice we just calculate the L2 distance between reconstructed images output from $\mu_{\mathbf{x}|\mathbf{z}}$ and the ground truth images as the loss function.

In the original VAE paper, the decoder was implemented as a Gaussian distribution with diagonal covariance structure, where the mean and covariance matrix with were both calculated with neural networks ³. There are also some implementations where the decoder is implemented as a Gaussian where the neural network is only concerned with calculating the mean and the covariance matrix is the identity matrix multiplied by some scalar $\sigma^2$, where $\sigma$ is a hyperparameter. In this scheme, the expectancy term is then replaced by a Monte-Carlo approximation that consists, most of the time, into a single draw, which evaluates to some scalar dependent on $ \sigma$ times the L2 distance between the mean of the Gaussian and the original input^{7 8 9 10}.

To train this entire setup, for every minibatch of input data, compute the ELBO forward pass using the reparametrization trick, backpropagation algorithm and an optimization algorithm such as stochastic gradient descent or Adam. This is seen in Algorithm 1. Notes on the backpropagation algorithm can be found in ⁵.

After training, we generate novel samples by sampling $\mathbf{z} \sim p(\mathbf{z})$, and the sampling $x \sim p_\theta(\mathbf{x} | \mathbf{z})$ ¹¹. This is seen in Algorithm 2.

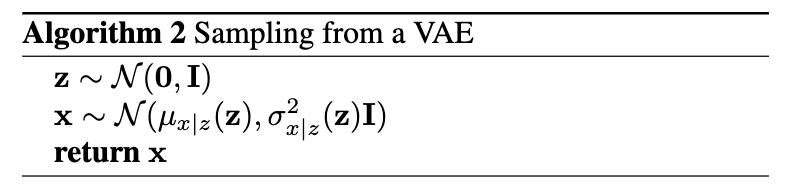
Advantages of VAEs over Vanilla Autoencoders

The loss function used to train VAEs can be thought of having “reconstruction term” (on the final layer), forces the encoder-decoder scheme to be as performant as possible, and a “regularisation term” (on the latent layer), that tends to regularise the organisation of the latent space by making the distributions returned by the encoder close to a standard normal distribution. The reconstruction term is the expected log likelihood of the data given a latent code, and the regularisation term is expressed as the KL divergence between the encoder and the prior.

Ideally, we want the latent space to exhibit continuity and completeness. Continuity corresponds to the notion that two points close in latent space should be similar to each other once decoded, and completeness corresponds to the idea that a point sampled from the latent space should give a meaningful output once decoded. The regularization term helps achieve this; it ensures that the covariance matrices are close to the identity matrix, which prevents punctual distributions, and is ensures that the mean is close to 0, which prevents encoded distributions to be too far apart from each other. With this regularisation term, we prevent the model to encode data far apart in the latent space and encourage as much as possible returned distributions to “overlap”, satisfying this way the expected continuity and completeness conditions. In vanilla autoencoders, this oragnization of the latent space is not guaranteed ².

References